
Plimpton 322 to słynna gliniana tabliczka, która od ponad 70 lat intryguje matematyków. Część z nich uważa, że jest ona dowodem na to, iż trygonometrię wymyślili nie Grecy, lecz Babilończycy. Czym w rzeczywistości jest to „jeden z najbardziej wyrafinowanych artefaktów naukowych starożytnego świata”?
Gliniany artefakt
Plimpton 322 to kawałek lekko obtłuczonej, glinianej tabliczki stosunkowo niewielkich rozmiarów (12,7 cm długości i 8,8 cm szerokości).
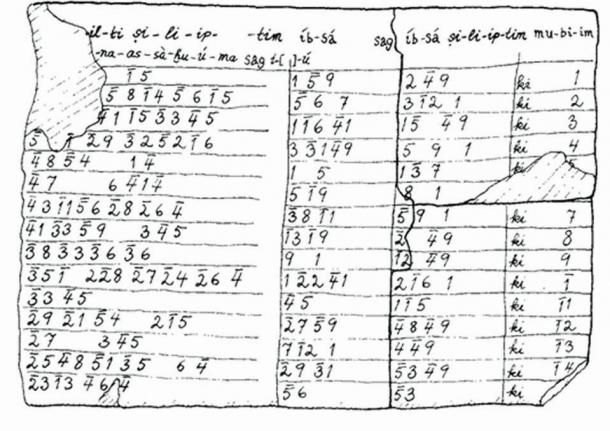
Po jednej stronie zapisana jest pismem klinowym, tworzącym ciąg 4 kolumn i 15 rzędów liczb w systemie sześćdziesiątkowym.
Tabliczka powstała ok. 1800 roku p.n.e., prawdopodobnie w starożytnym mieście Larsa w południowej Mezopotamii (obecnie stanowisko archeologiczne w Tell Senkereh w południowej części Iraku.
Jej odkrycie z początku XX wieku przypisuje się amerykańskiemu archeologowi i handlarzowi starożytnościami, Edgarowi Banksowi.
W 1922 roku kupił ją amerykański wydawca George Plimpton, który następnie w latach 30. przekazał tabliczkę Bibliotece Ksiąg Rzadkich i Rękopisów na Uniwersytecie Columbia w Nowym Jorku, gdzie przechowywana jest do dziś pod kryptonimem Plimpton 322 (P322).
Od tego czasu wielu uczonych próbowało odszyfrować tajemniczy zapis.
Udało się tego dokonać dopiero w 1945 roku dwóm matematykom Otto Neugebauerowi i Abrahamowi Sachsowi.
To właśnie oni jako pierwsi zauważyli, że liczby zapisane w poszczególnych wierszach odpowiadają trójkom pitagorejskim.
Matematycy stwierdzili, że Plimpton 322 była pomocą w rękach nauczycieli matematyki, ponieważ zawiera piętnaście trójek liczb całkowitych, których suma kwadratów dwóch z nich równa jest kwadratowi trzeciej (a2 + b2 = c2).
I nie byłoby w tym nic nadzwyczajnego, gdyby nie fakt, że tabliczka ta pochodzi sprzed tysiąca lat przed urodzeniem Pitagorasa.
Babilońska trygonometria
Temat tajemniczej tabliczki powrócił, kiedy dr Mansfield i prof. Wildberger z Uniwersytetu Nowej Południowej Walii w Sydney odkryli, że Plimpton 322 jest najstarszą starożytną tabelą trygonometryczną opartą na ułamkach.
Wnikliwe analizy tych dwóch australijskich matematyków wykazały, że na glinianej tabliczce w 15 wierszach opisano sekwencje 15 różnych trójkątów prostokątnych o coraz mniejszym nachyleniu.

Zdaniem naukowców w odłamanej części znajdował się dalszy ciąg zapisu, który pierwotnie tworzył 6 kolumn i 38 wierszy.
Uczeni zachwycają się fenomenem glinianej tablicy:
Wielką zagadką było, dlaczego starożytni skrybowie trudzili się, by stworzyć złożoną tablice
i uporządkować w niej liczby? Odkryliśmy, że Plimpton 322 opisuje trójkąty prostokątne za pomocą nowej trygonometrii bazującej na stosunkach względem siebie, a nie na kątach czy okręgach. To fascynująca praca genialnego umysłu – twierdzi dr Mansfield w artykule na temat Plimptona 322, który został opublikowany w piśmie „Historia Mathematica”.
A profesor Wildberger dodaje:
Tabliczka ta otwiera nowe pole do badań nie tylko przed historykami matematyki, ale może być przydatna również we współczesnej edukacji. To trygonometria prosta i dokładniejsza, na której możemy i my skorzystać. Istnieją olbrzymie zbiory babilońskich tabliczek, ale dotychczas zbadano niewielką część z nich. Świat matematyki dopiero się przekonuje, że starożytni mają na swoim koncie złożone osiągnięcia matematyczne, z których możemy wiele się nauczyć.
W swoim artykule matematycy zasugerowali, że Plimpton 322 na pewno nie był nauczycielską pomocą dydaktyczną.
Ich zdaniem Babilończycy wykorzystywali liczby z tabliczki do obliczeń architektonicznych przy budowie pałaców i świątyń oraz w pomiarach geodezyjnych.
Jeśli rzeczywiście byłaby to prawda, to można śmiało rzec, że wiedza Babilończyków była zaawansowana bardziej, niżby komukolwiek się to śniło.
